Наш общий бизнес-фронт BIKINIKA.com.ua
Гр а дусние вимір ення, високоточні астрономічні і геодезичні вимірювання, що виконуються на земній поверхні для визначення фігури і розмірів Землі. Сучасні Г. і. являють астрономо-геодезичні мережі , Службовці для обгрунтування топографічних зйомок (див. топографія ).
Геометричні основи Р. і. склалися в далекій давнині, коли виникло вчення про кулястість Землі і з'явилася практична необхідність у визначенні радіусу земної кулі для потреб астрономії, геодезії, географії і картографії. Спочатку Г. і. полягали у вимірі лінійної довжини S дуги меридіана між двома точками А і В, а також у вимірах в цих точках зенітної відстані z (див. небесні координати ) якого-небудь небесного світила s в меридіані (рис. 1). Шляхом зіставлення лінійної довжини S дуги меридіана і відповідного їй кута при центрі Землі, рівного різниці широт кінцевих точок цієї дуги і визначається за формулою:
j2 - j 1 = z2 - z1,
визначалася довжина D дуги земного меридіана:

звідки і виникло поняття про вимір градуса земного кола або про Р. і. Цим же способом визначався і радіус R земної кулі по формулі:

Перше в історії визначення радіусу земної кулі методом Г. і. було вироблено жили в Єгипті грецьким вченим Ератосфеном близько 250 до н. е. Знаючи, що опівдні в дні літнього сонцестояння Сонце в Сієні (нині Асуан) висвітлює дно глибоких колодязів, т. Е. Знаходиться в зеніті, а в Александрії відхиляється від зеніту на 1/50 частину кола, він визначив, що вимірюється в центрі Землі кутова відстань між цими містами дорівнює 7 ° 12 '. Лінійне ж відстань між тими ж містами, вважаючи їх лежачими на одному і тому ж меридіані, він визначив за часом і швидкості руху торговельних караванів і прийняв рівним 5 тис. Єгипетських стадій. Звідси він знайшов, що радіус земної кулі дорівнює 39 790 стадій, т. Е. 6311 км.
Одне з наступних Г. і. було вироблено араб. вченими в 827 за наказом багдадського халіфа Мамуна на рівнині між рр. Тигр і Євфрат під широтою близько 36 ° і грунтувалося на визначенні лінійної дуги меридіана шляхом безпосередніх вимірювань на місцевості і відповідного їй кута в центрі Землі по вимірах меридіанних висот одних і тих же зірок в її кінцевих точках. Це Г. і. показало, що довжина дуги меридіана в один градус дорівнює 112 км, т. е. дало для свого часу досить точний результат.
Після винаходу голландським ученим В. Снелліусом в 1615-17 методу тріангуляції з'явилася можливість вимірювати дуги меридіанів і паралелей будь-якої довжини. Застосувавши цей метод, французький учений Ж. Пікар в 1669-70 виробив Р. і. по дузі меридіана від Парижа до Ам'єна. Для вимірювання кутів тріангуляції він вперше застосував геодезичні інструменти із зоровими трубами, забезпеченими сіткою ниток.
У 2-ій половині 17 ст. було виявлено окремі факти і явища, які викликали нові наукові погляди на форму Землі як планети, що змінили завдання Р. і. Так, французький астроном Ж. Ріше виявив, що в Кайенне, розташованої в Південній Америці, поблизу екватора, годинник з маятником, вивірені в Парижі, відстають на 21/2 хв на добу і що для виправлення їх ходу необхідно укоротити маятник на 3 мм. Аналогічний факт встановив і англійський астроном Е. Галлей на о. Св. Олени в 1677. Пояснюючи ці факти, виходячи з закону всесвітнього тяжіння, І. Ньютон в 1680 висловив думку, що Земля не куля, а декілька сплюснута в напрямку осі обертання і має вигляд сфероїда. Припускаючи, що всі частинки маси Землі знаходяться в стані взаємного тяжіння, Ньютон теоретично визначив стискування земного сфероїда і отримав величину 1/230. Голландський фізик Х. Гюйгенс, припускаючи, що маси Землі притягуються тільки до її центру, в 1690 також визначив стискування земного сфероїда і знайшов величину 1/576. У 1691 з безпосередніх спостережень було відкрито стиснення планети Юпітер і тим же самим отримано наочний доказ можливою сфероїдічності планет Сонячної системи.
У зв'язку з виникненням точки зору про те, що Земля має форму сфероїда, який в найпростішому випадку є еліпсоїдом обертання, завдання Р. і. вже полягала у визначенні радіусу екватора а і полярного радіусу b Землі (рис. 2) або радіусу екватора і стиснення а земного еліпсоїда, т. е. величини

Довжина дуги S меридіана на еліпсоїді обертання і широти j 1 і j 2 її кінцевих точок пов'язані між собою рівнянням.

Якщо довжину дуги меридіана визначити з геодезичних вимірювань, наприклад методом тріангуляції, а широти її кінцевих точок - з астрономічних спостережень, то в наведеному рівнянні залишаться два невідомих а і а, що характеризують розміри земного еліпсоїда. Тому для визначення цих невідомих в принципі досить виконати Р. і. по двох дуг меридіана в різних географічних широтах. Але в дійсності для цієї мети використовуються Р. і. за численними дуг меридіанів і паралелей.
Щоб вперше визначити розміри земного сфероїда, т. Е. Довести сплюснутістю Землі в напрямку її осі обертання і обгрунтованість закону всесвітнього тяжіння, який ще викликав багато суперечок, французькі вчені Ж. Кассіні, Ж. Маральді і Ф. Лаир з 1684 по 1718 виконали Г . і. по меридіану від Парижа на північ до Дюнкерка і на південь до Перпиньяна. Однак це Г. і. не тільки не підтвердило теоретичних висновків про сплюснутости Землі в напрямку осі обертання, воно показало, навпаки, що вона витягнута в цьому напрямку. Помилковість цього висновку можна було пояснити помилками астрономічних і геодезичних вимірювань. Але тоді це було ще незрозуміло і тому викликало нові суперечки про справедливість закону всесвітнього тяжіння.
Для вирішення виниклих суперечок Паризька академія наук організувала дві експедиції по Г. і. в сильно розрізняються широтах, одна з яких була спрямована в Перу - до екватора, а інша до Лапландії - до Полярного кола. Перуанська експедиція під керівництвом П. Бугера за участю Ш. Кондамін і Л. Годена працювала з 1735 по 1742 і виміряла дугу меридіана завдовжки близько 3 °. Лапландська експедиція під керівництвом П. Мопертюї за участю А. Клеро і шведського фізика А. Цельсія (автора температурної шкали) працювала в 1736-37 і виміряла дугу меридіана всього лише близько 1 °. Результати робіт цих експедицій і Г. і. Кассіні у Франції остаточно довели як декомпозиція Землі, так і обгрунтованість закону всесвітнього тяжіння і мали величезне значення для розвитку геодезії і ін. Наук.
З 1792 по 1797 за розпорядженням революційного Законодавчих зборів Франції в розпал Великої французької революції було вироблено значне для свого часу Г. і. від Дюнкерка до Барселони. Це Г. і. вироблялося під керівництвом Ж. Деламбра і П. Мешена і послужило свого часу основою для встановлення довжини метра, як однієї десятимільйонна частини чверті дуги земного меридіана.
З початку 19 ст. астрономо-геодезичні роботи за програмою Г. і. стали проводитися в багатьох країнах з метою топографічного вивчення і картографування їх територій. З розробкою методів і винаходом приладів для визначення різниць довгот стали розвиватися Г. і. і вздовж земних паралелей. До теперішнього часу Г. і. зроблені в усіх країнах Європи. Розпочаті в 1800 англійськими геодезистами астрономо-геодезичні роботи в країнах Індостану поступово перетворилися в Г. і. і охопили значні території цих країн. Вжиті в 30-х рр. 19 в. астрономо-геодезичні роботи пізніше набули характеру Г. і. в США. Вони пов'язані нині (2-га пол. 20 ст.) З аналогічними роботами в Канаді і Мексиці, а також в деяких країнах Південної Америки. У 1883 англійськими геодезистами було розпочато в Африці Г. і. від мису Доброї Надії до Каїра, яке завершилося незабаром після 2-ї світової війни. В середині 20 ст. почалися роботи по Р. і. в Китаї, Австралії та ін. країнах. Розпочаті в кінці 20-х рр. 20 в. астрономо-геодезичні роботи в СРСР привели до сучасним Г. і. на великих просторах Європи та Азії.
У Росії Г. і. були розпочаті в 1816 К. І. Теінером в західних прикордонних районах і В. Я. Струве в прибалтійських губерніях. Розвиток цих робіт завершився виміром дуги меридіана від гирла Дунаю до берегів Північного Льодовитого океану завдовжки близько 25 ° 20 'по широті. У 19 столітті в Росії були проведені і інші астрономо-геодезичні роботи, які пізніше були замінені новими.
У міру накопичення матеріалів Р. і. з початку 19 ст. були проведені різні визначення розмірів земного еліпсоїда. До середини 19 ст. в цих визначеннях виявилися значні розбіжності, які не могли бути пояснені помилками Р. і. Намагаючись пояснити ці розбіжності, російський геодезист Ф. Ф. Шуберт в 1859 висловив думку про можливу трёхосності Землі і вперше визначив розміри земного еліпсоїда з трьома нерівними осями. Але уявлення Землі у вигляді тривісного еліпсоїда не усунув протиріч в результатах різних Р. і. Звідси виникло розуміння, що Земля має складний вигляд, і її фігура, за пропозицією ньому. фізика І. лістингу в 1873, була названа геоидом . З тих пір стали вважати, що завдання Г. і. полягає у визначенні розмірів земного сфероїда, найбільш правильно представляє фігуру геоїда, і відступів геоїда від цього сфероїда. Але виявилося, що вивчення фігури геоїда вимагає даних про внутрішню будову Землі і пов'язане зі значними труднощами. Щоб уникнути їх, сов. геодезист М. С. Молоденський в 1945 розробив теорії і методи визначення фігури фізичної поверхні і зовнішнього гравітаційного поля Землі.
В СРСР були проведені нові Г. і. і пов'язані з ними гравіметричні роботи. Широкий розвиток отримали також дослідження з визначення фігури, розмірів і гравітаційного поля Землі. У 1940 Ф. Н. Красовський і А. А. Ізотов отримали вельми важливі дані про розміри земного еліпсоїда, який під назвою еліпсоїда Красовського тепер застосовується в геодезичних роботах СРСР і ін. Соціалістичних країн (див. Красовського еліпсоїд ).
В даний час власне Р. і. використовуються переважно тільки для визначення розмірів Землі. Характеристики ж фігури Землі, а також її гравітаційного поля визначають за результатами вимірів сили тяжіння (див. гравіметрія ) І спостережень руху штучних супутників Землі (ШСЗ) і далеких космічних ракет (див. супутникова геодезія ) .При одночасному ж визначенні фігури, розмірів і гравітаційного поля Землі використовують спільно всю сукупність даних Р. і., Вимірів сили тяжіння і спостережень руху супутників.
Дані про фігуру, розміри і гравітаційне поле Землі мають велике значення для астрономії, геодезії, картографії та ін. Галузей знання. Вони входять до складу астрономічних і геодезичних постійних і широко використовуються для розрахунків по запуску ШСЗ і далеких космічних ракет.
Літ .: Струве В. Я., Дуга меридіана в 25 ° 20 'між Дунаєм і Льодовитим морем, т. 1-2, СПБ, тисячу вісімсот шістьдесят одна; Вітковський В. В., Практична геодезія, 2 вид., СПБ., 1911; Деламбр Ж. і Мешен П., Основи метричної десяткової системи або вимір дуги меридіана, укладеного між паралелями Дюнкерка і Барселони, пров. з франц., М. - Л., 1926; Михайлов А. А., Курс гравіметрії і теорії фігури Землі, 2 вид., М., 1939; Красовський Ф. Н., Керівництво по вищій геодезії, ч. 2, М., 1942; Ізотов А. А., Форма і розміри Землі за сучасними даними, «Тр. Центрального науково-дослідного інституту геодезії, аерозйомки і картографії », 1950, ст. 73; Молоденський М. С., Юркіна М. І. та Єремєєв В. Ф., Методи вивчення зовнішнього гравітаційного поля і фігури Землі, там же, 1960, ст. 131; Куликов К. А., Нова система астрономічних постійних, М., 1969.
А. А. Ізотов.

Мал. 2 до ст. Градусні вимірювання.
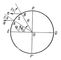
Мал. 1 до ст. Градусні вимірювання.